El concepto de estructura en una nueva concepción del proceso de enseñanza-aprendizaje de la Geometría
The structure concept in a new conception of the learning-teaching process
Dr.C. María Cristina González Dosil. Profesora Titular. Universidad de Ciencias Pedagógicas “Enrique José Varona”. La Habana, Cuba.
Correo electrónico: cristinagd@ucpejv.rimed.cu
MSc. Cosme Manuel Matías Burgos. Profesor Titular. Universidad de Ciencias Pedagógicas “Enrique José Varona”. La Habana, Cuba.
MSc. Alexis Almaguer Zayas. Profesor Auxiliar. Universidad de Ciencias Pedagógicas “Enrique José Varona”. La Habana, Cuba.
Recibido marzo de 2010 Aceptado mayo de 2010
RESUMEN En el artículo se plantea una manera novedosa e innovadora de enfocar el proceso de enseñanza-aprendizaje de la Disciplina Geometría sobre la base del concepto ampliado de estructura matemática. Ya Euclides y Hilbert, entre los siglos III a. n. e. y XX, propusieron una ordenación sistemática de la Geometría basada en un sistema de axiomas y F. Klein y S. Lie lo consiguieron en 1876, sobre la base del concepto de transformación del plano. La concepción que aquí se presenta, de acuerdo con las exigencias actuales, ofrece la ventaja de estudiar las geometrías sintética y analítica como modelos de la Geometría euclidiana. Los positivos resultados obtenidos se han podido corroborar en la práctica pedagógica de las asignaturas Geometría I y III, y en las investigaciones terminadas en la Universidad de Ciencias Pedagógicas “Enrique José Varona”. Por último, se plantean incógnitas que deben ser despejadas en futuras investigaciones. PALABRAS CLAVE: estructura, modelo, enseñanza, geometría. |
ABSTRACT This article poses a new and innovative manner in which to focus on the teaching learning process of the subject of geometry based on the concept of amplified mathematic structure. Already Euclid and Hiblert, in the III ann. and XX centuries proposed a new systematic order to Geometry based on a system of axioms and F. Klein and S. Lie finally were able to, in 1876, over the basis of the concept of transformations of planes. The conception that is presented within the article, according to current needs, offers the advantage of studying synthetically and analytical geometry as Euclidian geometrical models. The positive results asserted have been corroborated, in pedagogical practice, in the subjects of Geometry I and II and in the completed researches at the University of Pedagogical Sciences "Enrique Jose Varona." Lastly, further questions are posed that may be answered with future research in this area. KEY WORDS: structure, model, teaching, geometry. |
La investigación del proceso de obtención de los resultados científicos que forman parte de los contenidos de los cuales deben apropiarse, permite a los estudiantes llegar a la conclusión de que la Matemática, y en especial la Geometría, no están formadas por resultados acabados, sino que están en constante desarrollo. Este se genera mediante la resolución de los problemas que plantean al hombre los avances de la ciencia, la técnica y la sociedad, que a su vez condicionan el surgimiento de nuevos problemas.
El conocimiento de la historia tiene especial significación en la comprensión de la importancia y la aplicación posterior de los contenidos que se tratan en la carrera. La investigación de la evolución de la ciencia matemática aporta elementos valiosos para comprenderla; no obstante, el objeto de estudio de esta ciencia difiere del de su enseñanza, pues ambas responden a distintos encargos sociales. Los estudiantes no solo deben apropiarse de los principales resultados, sino también de las formas de trabajo y pensamiento que caracterizan el trabajo matemático, a partir de lo cual deben estar en condiciones de adquirir otros conocimientos de forma independiente. La resolución de problemas tiene un papel fundamental en el logro de este objetivo, pues constituye el centro de la actividad matemática y puede ser utilizada en el proceso de enseñanza-aprendizaje de esta disciplina, con el fin de promover la actividad productiva de los estudiantes.
El trabajo científico metodológico y científico investigativo de los docentes de la disciplina de Geometría en la Universidad de Ciencias Pedagógicas “Enrique José Varona” (UCPEJV) ha estado dirigido a potenciar, mediante el estudio de esta disciplina, por las vías sintética y analítica, las formas de trabajo y pensamiento propias de la actividad matemática. En el presente artículo se pretende mostrar una concepción del desarrollo actual de esta disciplina, sobre la base de la aplicación del concepto de estructura matemática, que sistematiza los resultados del trabajo de los docentes. Para ello se han considerado la generalidad de este concepto, la posibilidad de ordenar el contenido, según diferentes tipos de modelos, el carácter heurístico de sus razonamientos, así como sus potencialidades para la aplicación de estrategias metacognitivas, a fin de contribuir a la formación de la concepción científica del mundo. Como es conocido, fueron los egipcios y los babilonios los primeros en desarrollar una Matemática-geométrica primitiva. La Geometría fue creada por topógrafos y carpinteros como consecuencia de las periódicas inundaciones del gran río Nilo y las necesidades prácticas de las construcciones.
Sin embargo, fueron los filósofos clásicos griegos los que, basados en los resultados alcanzados entre los siglos VI y III a.n.e., sentaron las bases de una arquitectura definitiva de abstracción y demostración deductiva. Para ello, seleccionaron la Geometría euclidiana con su amplia estructura y la aplicaron a la comprensión del Universo. De esta manera surgían los gérmenes de dos corrientes filosóficas contrapuestas que impregnaron la Matemática y su enseñanza: el Intuicionismo y el Formalismo: la primera fue fundada por Brower L (1881-1968); según refiere el investigador Pino C, esa corriente preconizaba que “… en la Matemática la idea de existencia es sinónimo de constructividad y la idea de verdad es sinónimo de demostrabilidad”.1
Por otra parte, el Formalismo de Hilbert D (1885-1945), como afirma Pino C, defendía la idea de que la Matemática “…es una creación de la mente humana y consiste solamente en axiomas, teoremas y definiciones combinados de acuerdo a ciertas reglas o convenios pre establecidos”.2
El desarrollo de la Geometría griega se debió esencialmente a las dificultades de estos sabios para comprender el concepto de número irracional, número mágico caprichoso e irrespetuoso, que no era ni entero ni racional, ni el cociente entre dos enteros, como lo demostraba el teorema de Pitágoras aplicado al triángulo rectángulo e isósceles de catetos de longitud 1 e hipotenusa
Tendrían que transcurrir casi veintitrés siglos de descubrimientos, estudios e investigaciones para que la Geometría alcanzara su estatus actual en los currículos de Matemática, especialmente en la formación de profesores.
De esta manera, durante una larga etapa comprendida entre los siglos III a.n.e. y el XX, se desarrollaron dos grandes corrientes que tenían como objetivo ordenar la Geometría y su enseñanza de modo sistemático: la axiomática, liderada por Euclides y Hilbert, en 1899, y la construcción mediante transformaciones del plano cuyos abanderados fueron F. Klein y S. Lie, en 1876. Ambas concepciones significaron en su momento un gran aporte científico y metodológico al desarrollo de la Geometría pero que, como es comprensible, no satisfacen hoy día completamente las exigencias del proceso de enseñanza-aprendizaje de esta disciplina.
Sin embargo, los métodos que utiliza la ciencia para elaborar las teorías no coinciden, de manera general, con los métodos de apropiación de estos conocimientos. “Hay que destacar con suficiente fuerza, el hecho de que la enseñanza de la Matemática no puede ser un reflejo de la ciencia Matemática, ya que ambas son ciencias de naturaleza diferente y que se diferencian en sus objetos, objetivos y tareas. Con lo dicho resulta claro que el contenido y las funciones de la enseñanza de la Matemática no están determinados solamente por la ciencia Matemática, sino que dependen fundamentalmente del encargo social de la educación y el lugar que corresponde ocupar a los alumnos en la sociedad”.3
Este planteamiento es de vital importancia, el conocimiento de la ciencia Matemática, en particular de la Geometría, constituye una premisa ineludible para todo profesor que se dedique a ella, pero no es suficiente para tener éxito en su enseñanza. Por ello, resulta de incuestionable valor conocer cómo ha evolucionado el proceso de enseñanza-aprendizaje de esta disciplina en la Universidad de Ciencias Pedagógicas “Enrique José Varona”, desde los inicios de la formación de profesores hasta la actualidad. Ello da la posibilidad de determinar cómo se ha desarrollado este proceso y cuáles son las problemáticas que enfrenta en la actualidad.
El estudio de la disciplina Geometría en la formación de profesores de Ciencias Exactas se realiza mediante el método axiomático, el cual suministra una estructuración lógica que no se reduce a los elementos lógico-formales, presentes en la relación interna entre sus proposiciones y demostraciones. La evolución y el desarrollo de este método expresa el perfeccionamiento de las teorías matemáticas, en calidad de instrumentos para una investigación flexible y dialéctica de los procesos del mundo real.
La disciplina está conformada por tres asignaturas: Geometría I, Geometría II y Geometría III. En la primera se aborda la Planimetría y se fundamenta, mediante un sistema de axiomas, la Geometría Euclidiana, estudiada en niveles precedentes. En la Geometría II se trata la Geometría Analítica como un modelo de la Geometría Euclidiana, con lo cual se da a los estudiantes la posibilidad de resolver analíticamente problemas ya tratados por métodos sintéticos, demostrando así las ventajas de esta vía de solución. En esta asignatura se integran el Álgebra y la Aritmética con la Geometría para contribuir a resolver los dos problemas fundamentales de esta:
- Dada una ecuación, interpretarla geométricamente; es decir, construir la gráfica correspondiente.
- Dada una figura geométrica, o la condición que deben cumplir sus puntos, determinar su ecuación.
- Los conocimientos y las habilidades que adquieren los estudiantes con esta asignatura son utilizados posteriormente por las disciplinas de Análisis y Álgebra.
La asignatura de Geometría III se dedica al estudio de la Geometría del Espacio; con su desarrollo se extiende al espacio la construcción axiomática de la Geometría que se inicia en los programas precedentes y, con ella, finaliza esta construcción. En todas las asignaturas de la disciplina se mantiene el estrecho vínculo con la Geometría Escolar, pues tienen gran incidencia en los programas escolares, debido a que brindan métodos y formas de trabajo que influyen directamente en el desarrollo de capacidades mentales generales y específicas en los alumnos.
Las razones planteadas condujeron a los autores, apoyados en su experiencia de más de 30 años como docentes, y en investigaciones consultadas y realizadas, a concebir el desarrollo actual de esta disciplina, sobre la base del concepto de “estructura matemática”. La bondad de esta concepción novedosa se justifica en buena medida por:
-La generalidad de este concepto, que permite definir, de manera sencilla, el concepto de modelo que se utiliza; por ejemplo, en la llamada Geometría Analítica y aplicarlo en diferentes situaciones matemáticas.
- La Geometría (en los diferentes niveles educacionales) puede ordenarse según el estudio de estructuras de incidencia, afines, métricas y topológicas.
- Las posiciones relativas entre diferentes objetos geométricos y sus relaciones pueden aplicarse de manera creativa mediante procedimientos, estrategias heurísticas y metacognitivas a la resolución de los distintos tipos de problemas geométricos.
- La posibilidad que brinda de ofrecer una visión sencilla, integral y abierta de esta ciencia, como reflejo de la realidad objetiva.
Para una mejor comprensión de lo expresado, a continuación se plantea el concepto de estructura matemática:
Por una estructura matemática se entiende el n-uplo
E = (C1, C2, C3… Cm, Rm+1, Rm+2, R m+3,…, R n)
en el cual los primeros m elementos son conjuntos no vacíos, llamados soportes de la estructura, dados en un cierto orden, y los restantes n-m elementos son conjuntos de relaciones que se establecen entre los elementos de estos conjuntos.
Algunos ejemplos de estructuras que se estudian en la Geometría son:
1. E i= (p,Â, I) llamada estructura de incidencia para el plano.
2. E a = (p,Â, I, // ) llamada estructura de plano afín.
3. E v = (V,Â,+, •) estructura combinada llamada espacio vectorial.
p, Â, I representan, respectivamente, el conjunto de puntos del plano, el conjunto de rectas del plano y la relación de incidencia entre puntos y rectas en el plano. En el segundo ejemplo: // designa la relación de paralelismo entre rectas en el plano, y en el tercero (V, Â, +, •), representan, en ese orden, el conjunto de vectores del plano, el dominio de los números reales y las operaciones de adición (interna en V) y multiplicación (externa en Â).
De manera análoga, otros contenidos geométricos pueden ser expresados mediante este concepto, que como puede observarse, se destaca por su sencillez y elegancia, con el consabido ahorro de recursos matemáticos.
Lo expuesto anteriormente conduce, de manera directa, al planteo de las preguntas siguientes: ¿será posible extender esta concepción a estructuras que combinen contenido con métodos, estrategias, modos de pensar y de actuar en el proceso de enseñanza-aprendizaje de la Geometría? Y en caso dado: ¿se justificará la ganancia metodológica?
A criterio de los autores la respuesta a tales interrogantes se encuentran en:
1. La práctica pedagógica.
2. La investigación educativa.
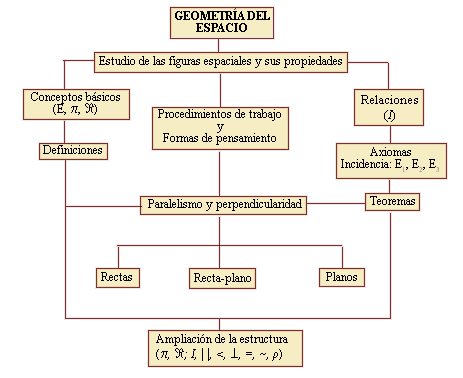
La primera interrogante se ha respondido afirmativamente en el desarrollo de las asignaturas Geometría I y III de la carrera de Ciencias Exactas, mediante su perfeccionamiento continuo en esa dirección. Las figuras 1 y 2 ilustran cómo se concibe, sobre esta base, el tratamiento de la Geometría Plana (Geometría I) y de la Geometría del Espacio (Geometría III).
Para el estudio de la Geometría Plana (Geometría I) se parte de la estructura (p, Â; I,< ), donde p y  son los conjuntos bases o soportes de la estructura, que representan, respectivamente, el conjunto de puntos del plano y el conjunto de rectas del plano; I y < representan las relaciones de incidencia y orden. Sobre la base de esta estructura se formula el sistema de axiomas de la Planimetría, que a su vez sirve de base para la elaboración de la construcción axiomática correspondiente. Como consecuencia, se obtiene una nueva estructura (p, Â, I; <, II, ^, =, ~ , r), que incluye ahora las relaciones de paralelismo (II), perpendicularidad (^), igualdad (=), semejanza de figuras (~), medición (r) y procedimientos y formas de pensamiento (p) (Fig. 1).
Para la Geometría del Espacio (Geometría III), se considera inicialmente la estructura (E, p, Â; I ), en la cual se consideran como conjuntos bases E, p, Â que representan respectivamente el conjunto de puntos del espacio, el conjunto de planos del espacio y el conjunto de rectas del espacio. La construcción de la Estereometría se elabora de forma análoga a como se realizó para el plano y se obtiene finalmente la estructura (E, p, Â; I, <, II, ^, ~ , r, p) en la cual se han ampliado al espacio las relaciones definidas anteriormente para el plano (Fig. 2). En ambos casos puede observarse que es posible, de manera natural y didáctica, integrar a la estructura los métodos, procedimientos, estrategias heurísticas, metacognitivas, formas de pensar y modos de actuación, que permiten potenciar la Geometría y considerarla no solo como una disciplina más del currículo, sino como la expresión más elaborada del pensamiento lógico en el lenguaje de las matemáticas.
En este proceso se dedica especial atención al planteamiento de problemas que promuevan en los estudiantes la necesidad de dar respuesta a situaciones que para las cuales, no son suficientes los conocimientos con que cuentan hasta ese momento.
Este proceder resulta de un alto valor formativo, pues muestra la Geometría como una ciencia en constante desarrollo, estrechamente vinculada con la práctica, y potencia la formación de valores morales relacionados con el modelo del profesional de la educación que se pretende formar en la carrera.
Fig. 1. Estructura de la asignatura de Geometría I. Elaboración propia. Fig. 2. Estructura de la asignatura de Geometría III. Elaboración propia. La segunda interrogante ha sido respondida parcialmente en las tesis doctorales y de maestrías realizadas en el marco de la disciplina Geometría en el Departamento de Ciencias Exactas, así como en dos investigaciones terminadas. Las temáticas abordadas están en relación con el perfeccionamiento del proceso de enseñana-aprendizaje de la Geometría, en especial con la aplicación del concepto de reflexión, la organización del conocimiento en Geometría, la comprensión en las demostraciones geométricas, la problematización del conocimiento, la representación y la imaginación espacial. No obstante, para completar los estudios en cuanto a la validación de tal concepción, será necesario investigar sobre los problemas actuales siguientes:
- La sistematización de los resultados de las investigaciones realizadas en la disciplina.
- La importancia de la aplicación del principio metodológico del historicismo en el desarrollo de la Geometría.
- Problemas epistemológicos en el estudio de las relaciones plano-espacio y espacio-espacios.
- Las relaciones de colinealidad y la aplicación de los teoremas de Ceva, Menelao y Desargues. De acuerdo con las exigencias actuales del perfeccionamiento continuo del proceso de enseñanza-aprendizaje de la Geometría, resulta posible y ventajoso su ordenamiento, de manera novedosa, sobre la base del concepto de estructura matemática. El trabajo metodológico que desarrolla la disciplina de Geometría del Departamento de Ciencias Exactas de la Universidad de Ciencias Pedagógicas ‘‘Enrique José Varona’’ ha estado encaminado en esta dirección. Resultados de tal concepción se observan en el desarrollo de las asignaturas Geometría I y III.
La investigación educativa realizada por los docentes también ha dado respuesta a esta problemática; no obstante, resulta evidente la necesidad de continuar trabajando en este sentido, a partir de las regularidades constatadas en la disciplina.
Medellín, Colombia, 1997. Página 2. 1PINO C, CARDEÑO J. La enseñanza de la Geometría. Medellín, Colombia: Editora CEID-Addida; 1997. p. 2.
2PINO C, CARDEÑO J. La enseñanza de la Geometría. Medellín, Colombia: Editora CEID-Addida; 1997. p. 2.
3HERNÁNDEZ H. Didáctica de la Matemática. Artículos para el debate. Quito, Ecuador: Escuela Politécnica Nacional; 1993. p. 3. CASTELLANOS B. La visión humanista de la educación y el aprendizaje. Soporte electrónico. La Habana, Cuba: Instituto Superior Pedagógico “Enrique José Varona”; 2001.
CASTRO S, ET AL. Geometría. La Habana, Cuba: Editorial Pueblo y Educación; 1985.
EFIMOV N V. Geometría Superior. Moscú: Editorial Mir; 1984.
GONZÁLEZ M. Propuesta didáctica para la aplicación de la enseñanza basada en problemas a la formación semipresencial en la disciplina de Geometría. [Tesis en opción al Grado Científico de Doctor en Ciencias Pedagógicas]. La Habana, Cuba: Instituto Superior Pedagógico “Enrique José Varona”; 2006.
MATÍAS C. Criterios didácticos que sustentan los fundamentos de las transformaciones del plano. [Tesis en opción al Título Académico de Máster en Didáctica de la Matemática]. La Habana, Cuba: Instituto Superior Pedagógico “Enrique José Varona”; 1999.
MULLER H. Zur komplegitat von Beweisen in Mathematikunterricht. In: Beitrage zum Matematitunterricht. Potsdam, Alemania: 2001.
PONTRIAGUIN L S. Grupos continuos. Moscú: Editorial Mir; 1978.
YAKOLIEV G N. Geometría. Moscú: Editorial Mir; 1985. Introducción
Desarrollo
![]() Entonces, los griegos resolvieron este problema desterrándolo y creando así, una Geometría llamada pura o sintética, término este último bastante desafortunado, como se comprobaría más tarde.
Entonces, los griegos resolvieron este problema desterrándolo y creando así, una Geometría llamada pura o sintética, término este último bastante desafortunado, como se comprobaría más tarde.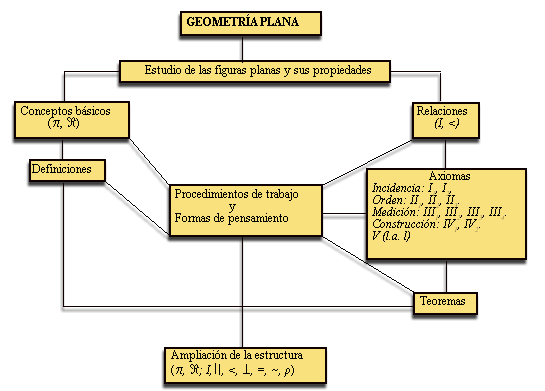
Conclusiones
Referencias
Bibliografía